ENERGETIC METHODOLOGIES OF STRUCTURAL INTERACTIONS IN PHYSICO-CHEMISTRY
ENERGETIC METHODOLOGIES OF STRUCTURAL INTERACTIONS IN PHYSICO-CHEMISTRY
Abstract
Entropic principles provide a basic foundation for the formation of functional relationships between many quantities of chemical kinetics. The equilibrium sum of entropic components of the universal gas constant, equal to R/2, has a direct mathematical relationship with the tangent of the geodesic angle. A similar relationship of this parameter is obtained from Arrhenius graphs – the dependence of the reaction rate coefficient on temperature. When two entropic components move in one format, the equilibrium sum of their energies is equal to half of the initial energy value. The established principles are also manifested in other regularities of chemical kinetics and physics, for example, in the activation energy of diffusion processes and in the kinetic energy equation.
1. Введение
Известно , , что понятие энтропии, вытекающее из второго закона термодинамики, является критерием направленности процесса в системе и степенью упорядоченности самой системы молекул или атомов. Если в этих системах их взаимодействие идет по направлению градиента потенциала – положительная работа, то результирующая потенциальная энергия и приведенная масса находятся по принципу сложения обратных величин соответствующих значений (величин подсистем). Такой процесс является корпускулярным, теоретической концепцией которого и являться энтропия. С другой стороны – в системах, в которых взаимодействие идет против градиента потенциала – отрицательная работа, выполняется алгебраическое сложение их масс и энергий, что характеризуется волновым процессом, теоретической концепцией которого может являться негэнтропия. Резонансное стационарное состояние в системе достигается при условии равенства этих энтропийных составляющих – энтропия полностью компенсируется негэнтропией .
Цель работы – установить функциональные количественные связи между энтропией и энергетическими величинами структурных взаимодействий в физико-химии.
2. Энтропия и универсальная газовая постоянная
Газовую постоянную называют универсальной по ее многоплановому применению в химической кинетике и физике. Так, по уравнению состояния газа универсальная газовая постоянная R равна работе расширения 1 моля газа при увеличении температуры на 1⁰ K. А в химической реакции R равна разности молекулярных теплоемкостей при постоянном давлении и объеме газа.
По уравнению Больцмана:
где S – энтропия, k – постоянная Больцмана, w – число доступных состояний.
Заменяя lnw на число Авогадро (А) получаем:
Исходя из уравнения (2), газовую постоянную R можно рассматривать как параметр энтропии, имеющий максимальное значение для любого процесса или системы взаимодействующих молекул или атомов.
В общем случае при поступательном движении системы из двух одинаковых по величине векторов () с разностью фаз 90° их равнодействующая определиться:
Если происходит вращательное движение или движение по спиральной динамике, то вектор () станет касательным вектором и образует угол вращения, для которого с учетом (2) можно записать:
Подставив в (3) выражение (2) получим:
Если принять угол φ как геодезический угол, равный 54,733°(под этим углом, например, тутовый шелкопряд наматывает нить на основу), то получим tgφ=1.4141, т.е. величину достаточно близкую к величине, полученной по зависимости (4). На основании этого можно записать:
Для уточнения уравнения (7) введем квантовую поправку aо=1,00233:
Таким образом, параметр R∙1/2 есть равновесная энтропийная составляющая равная 50% от максимального значения R, натуральный логарифм которого численно равен тангенсу геодезического угла с учетом квантовой поправки ао.
3. Энтропийные номограммы
В работе для оценки степени структурных взаимодействий предложен обменный гамильтониан, полученный в предположении о прямом перекрывании волновых функций взаимодействующих атомов:
где: – спиновый оператор изотропного обменного взаимодействия для пары атомов, I0 – постоянная обмена, S1 и S2 – интегралы перекрывания волновых функций.
Интегралы перекрывания волновых функций моделируются в работе через величину относительной разности энергетических параметров взаимодействующих атомов – коэффициент α (в %). Данный параметр является прямой характеристикой степени энтропийного равновесия в системе. Покажем это на примере номограммы (рис. 1) – зависимости степени структурных взаимодействий (ρ,%) от коэффициента α (%), полученной в работе для широкого класса структур.
Из номограммы следует, что при изменении α от 0 до 5% условия взаимодействия атомов соответствуют условиям энтропийного состояния, при котором =100% и соответствует неограниченной взаимной растворимости атомов взаимодействующих компонентов в твердом состоянии, т.е. максимальной степени волновой составляющей взаимодействия.
Увеличение значений α (рис.1) характеризует нарастание корпускулярных и электростатических свойств атомов одного химического элемента между собой, что приводит к их ограниченной растворимости в атомах другого химического элемента. Для равновесного энтропийного состояния данной системы можно записать (в линейной интерпретации):
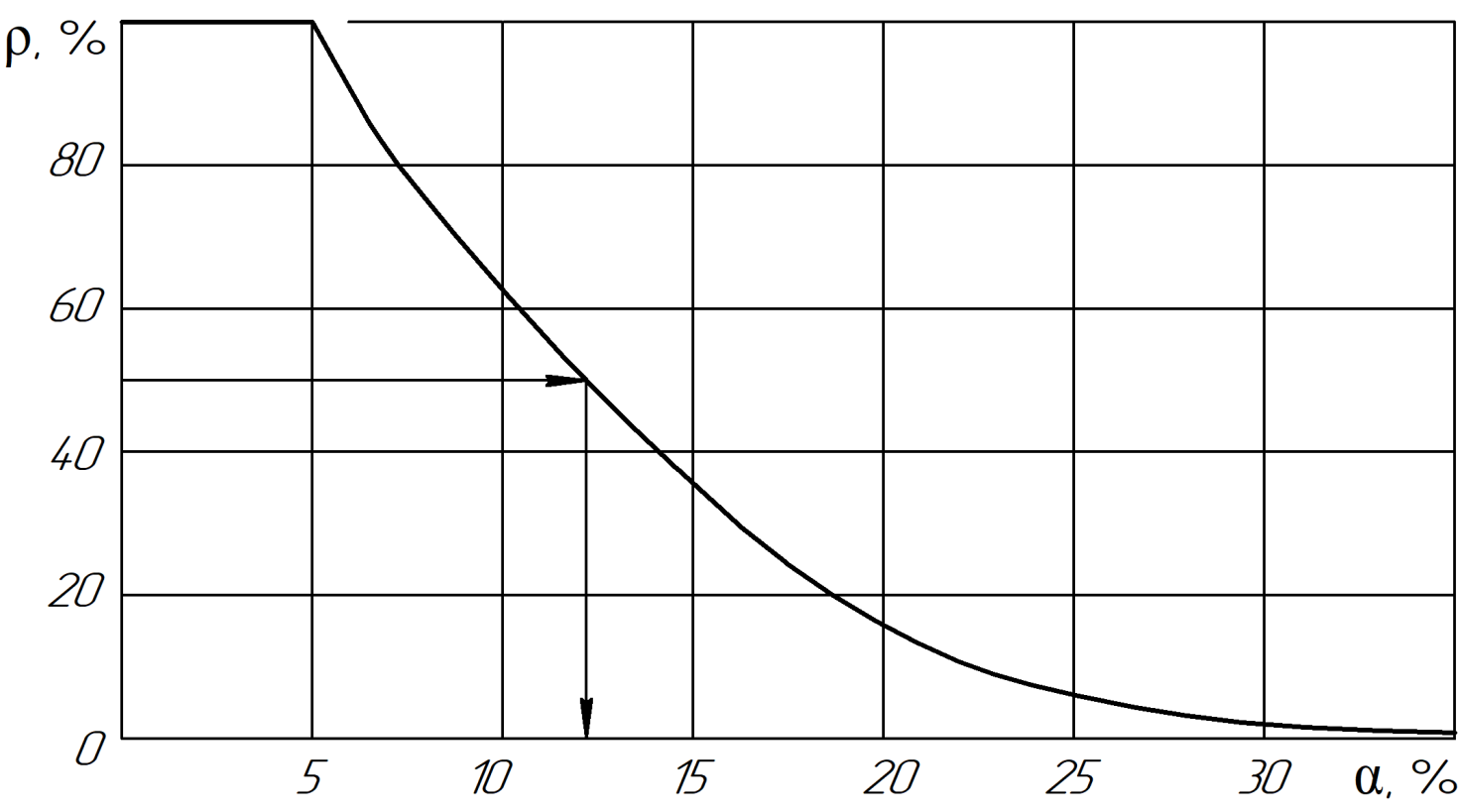
Рисунок 1 - Зависимость степени структурных взаимодействий (ρ) от коэффициента α
4. Энтропия по уравнениям графика Аррениуса
В химической кинетике нередко при исследованиях используются значения средней температуры опыта. Такая методика применяется, например, для оценки энергии активации и предэкспоненциального множителя в уравнении Аррениуса. Можно предположить, что данный подход эквивалентен применению аналогичной величины R∙1/2, определяемой по уравнению (7). Для этого рассмотрим не логарифмический вариант графика зависимости коэффициента скорости химической реакции (Кр) от температуры (Т) (рис. 2).
Данный график аналогичен приведенному выше. В середине графика есть точка, по которой на оси абсцисс есть значение температуры равное примерно 628 К. Она равна среднему значению температуры опыта, то есть 50% от ее максимального значения. На оси ординат ей соответствует значение Кр=17⋅10-4. Значение 50% можно применять в расчётах энтропийных соотношений, но только для негэнтропийной составляющей графика.
Для коэффициента скорости необходимо иметь ее значение в относительных величинах (в процентах). Для этого применим корреляцию коэффициента Кр (по рис.2) со значением a на номограмме (рис.1). По соотношению их максимальных значений, коэффициент корреляции равен 35/50»0.7, поэтому: 17××0.7»11.9a%. Получается уравнение, аналогичное уравнению (5):
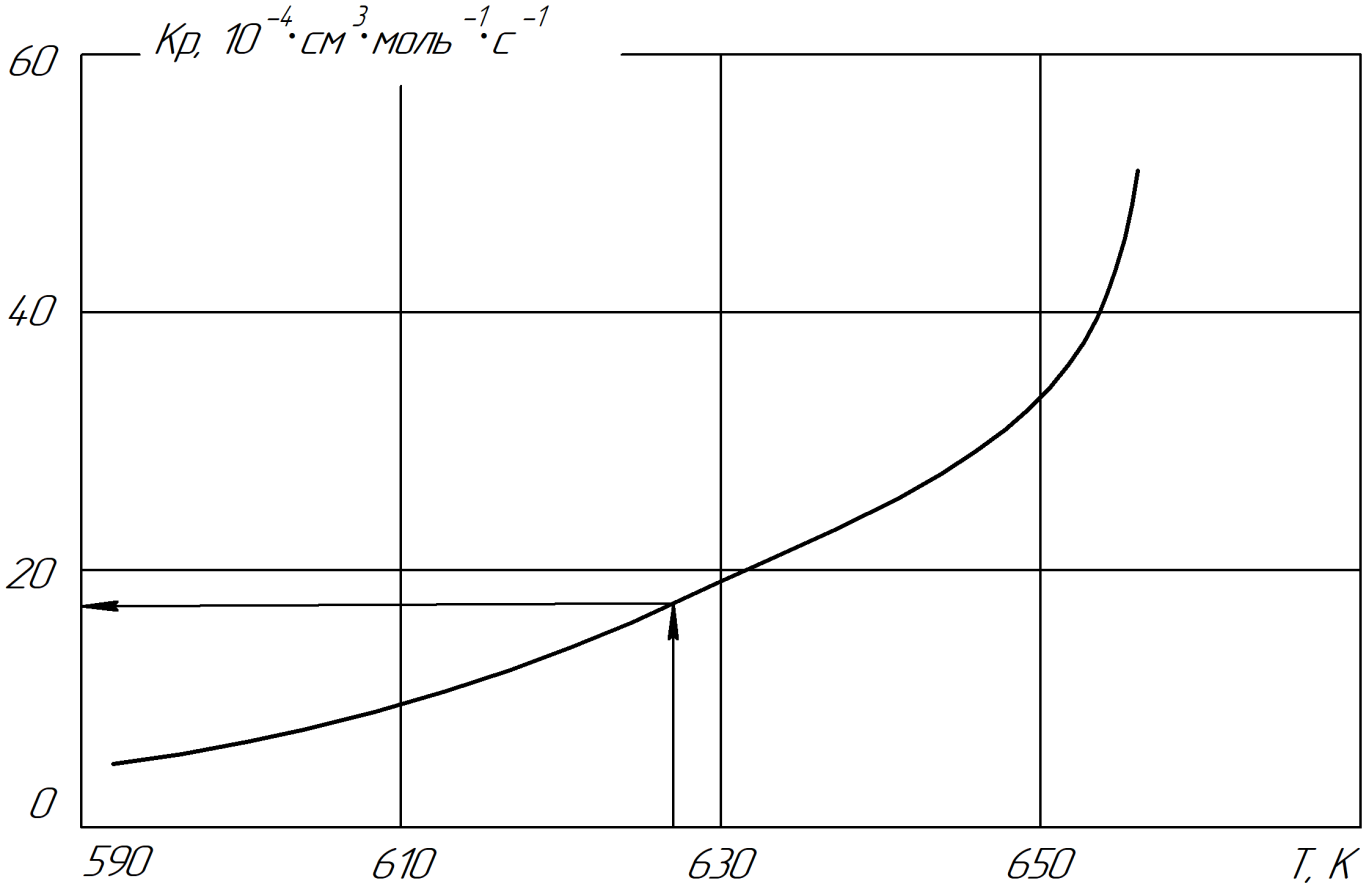
Рисунок 2 - График зависимости коэффициента скорости (К) от температуры (Т)
Примечание: по ист. [4]
5. О факторе электронной концентрации атомов
Известно, что при заданной температуре из двух конкурирующих между собой состояний системы взаимодействующих разнородных атомов устойчиво будет то, которое обладает меньшей свободной энергией . Так энтропия однофазного твердого раствора компонента А в компоненте В (SАВ) всегда выше, чем энтропия SА-В того же сплава, распавшегося на два твердых раствора А и В разной концентрации. Если при этом UАВ < UА-В, то однофазное состояние раствора устойчиво при всех температурах. Если UАВ > UА-В, то при высоких температурах устойчиво состояние двухфазного раствора, а при низких – однофазного. Учитывая взаимодействие между одними лишь ближайшими соседними атомами в кристаллической решетке и не принимая во внимание её упругой деформации, обусловленной различием атомных радиусов химических элементов, условие образования непрерывного ряда твердых растворов выразится :
где UАА, UВВ и UАВ – энергии связи чистых компонентов и их раствора соответственно.
Если 2UАВ > UАА+UВВ, то это означает более сильное взаимодействие между собой одинаковых атомов, чем атомов А с атомами В. Очевидно это связано со строением атомов химических элементов, и в первую очередь с их электронной концентрацией (e/a) – среднее число валентных электронов (e), приходящихся на один атом (a).
Юм-Розери установил, что электронная концентрация однотипных фаз одинакова у всех систем. Так, b – фазы с объемно-центрированной кубической (ОЦК) решеткой и b – фазы с примитивной решеткой (типа CsCl) образуются при электронной концентрации, близкой к 3/2, фазы типа γ-латуни при е/а≈21/13, а ε – фазы с гексагональной плотноупакованной решеткой (ГПУ) – при е/а≈7,4. Объяснение этих особых значений электронной концентрации было дано Джонсом на основе представлений о зонах Бриллюэна. В зоне Бриллюэна имеется место лишь для определенного числа электронов при данном типе структуры. Добавочные электроны могут встроиться в решетку лишь с дополнительной затратой энергии. Вследствие этого более выгодной и более устойчивой окажется новый тип структуры с более высокой предельной концентрацией валентных электронов.
После опубликования работ Юм-Розери и Джонса было найдено, что составы многих металлических фаз обнаруживают, по крайней мере, частичную зависимость от электронной концентрации. Но соотношения между протяженностью твердых растворов и е/а - для них не выполняются. Последнее обстоятельство говорит о том, что фактор электронной концентрации является не единственным и даже не главным фактором фазообразования металлических систем. Данный вывод следует из энтропийных принципов, которые применимы и к атомной структуре. Изначально атом представляет собой систему двух противоположных начал единой действительности. Кинетическая энергия орбитального движения проявляется как негэнтропия, а потенциальная энергия атомного ядра – как энтропия. Энтропийно-равновесное состояние этих составляющих дает стабилизацию атомной структуре в соответствии с уравнением Планка. При этом суммарная энергия атомного центра, рассчитанная по принципу сложения обратных величин исходных составляющих, дает наиболее эффективную энергию каждого атома и может применяться при решении практических задач в материаловедении .
6. Уравнение энергии активации диффузии и самодиффузии
С учетом исходных принципов энтропии, результирующую величину эффективной энергии парного взаимодействия атомов А и В, тождественную энергии активации процесса диффузии, получим в виде суммы обратных величин Р-параметров:
где Еа – энергия активации процесса диффузии атома В среде атомов А; n - число всех валентных электронов, или число наиболее удаленных от ядра валентных электронов конкретного атома.
Цифра 2 в этом уравнении дает среднюю равновесную сумму по каждому атому. Здесь величина , где Рэ – пространственно-энергетический параметр, численно равный эффективной энергии структурных взаимодействий.
Р-параметр был получен в работе путём применения принципов сложения энтропийных составляющих разноименно заряженных систем (принцип сложения обратных величин). В данном случае – это энергия атомного ядра и орбитальная энергия электронов.
При диффузии атома В в однородной по составу и подобной ему среде с атомами В значение Еа приобретает смысл энергии активации самодиффузии атома В. Исходя из (12) она определяется:
Цифру 4 можно рассматривать как произведение двух цифр 2. Одна цифра 2 в знаменателе этого уравнения учитывает среднюю равновесную сумму для каждого атома. Другая цифра 2 – соответствует принципу сложения обратных величин двух одинаковых Р-параметров.
Сопоставление результатов расчетов с экспериментальными данными показало их удовлетворительное совпадение .
Таким образом, во всех рассмотренных примерах равновесная сумма энтропийных составляющих равна половине суммы максимальной первоначальной величины их энергий.
7. Заключение
1. Равновесная сумма энтропийных составляющих универсальной газовой постоянной, равная R/2, имеет прямую математическую связь с тангенсом геодезического угла.
2. Аналогичное соотношение этого параметра получено по графикам Аррениуса – зависимости коэффициента скорости химической реакции от температуры.
3. Установленные принципы проявляются и в других закономерностях физикохимии, например, в энергии активации диффузионных процессов, и могут применяться при решении практических задач в материаловедении.
