Acceleration and Deceleration of the Gas Flow under Different Influences
Acceleration and Deceleration of the Gas Flow under Different Influences
Abstract
The effects on the gas flow during its movement in the elements of aircraft engines construction are examined. Possible effects on the flow are presented, among which are geometric, flow, thermal, mechanical and friction effects. Partial equations are analysed in relation to each type of effect. The physical influence of the effect of each influence on the flow for its acceleration and deceleration is presented. The influence of each of the effects on the character of velocity change of subsonic and supersonic flows is studied. Practical implementations of effects on the flow in various aircraft engines are specified. The necessity of taking into account the simultaneous effect of several influences on the gas flow in the elements of a gas turbine engine is shown.
1. Введение
В общем случае при движении газового потока на него может быть оказаны следующие воздействия: механическое, тепловое, расходное, геометрическое. Перечисленные воздействия относятся к внешним. Кроме того, при движении потока трение рассматривается как внутреннее воздействие.
В элементах конструкции авиационных двигателей летательных аппаратов газовый поток, используемый в качестве рабочего тела, подвержен целому ряду воздействий. Таковыми являются геометрическое, тепловое, механическое, расходное воздействия и воздействие трения
, . Геометрическое влияние (F≠const) объясняется тем, что рабочая часть конструктивных элементов обычно представляет собой канал (или сочетание каналов) с различными площадями поперечных сечений. Тепловое (qвнеш ≠0) и механическое (lвнеш ≠0) воздействия имеют место при наличии энергообмена между потоком газа и окружающей средой, осуществляемого соответственно в форме теплоты и работы. Расходное воздействие (G= const) будет происходить тогда, когда от потока отбирается или к нему подводится какая-то масса газа. И, наконец, влияние трения (lтр ≠0) имеет место всегда, так как трение является неотъемлемым процессом при течении газового потока, обладающего свойством вязкости.2. Основные результаты
Рассмотрим движение идеального газа, полагая, что поток подвергается геометрическому, тепловому, механическому, расходному воздействиям и влиянию трения, т.е. полагаем, что F ≠ const; qвнеш ≠ 0; lвнеш≠0 ; G≠0; lтр≠0
.При указанных условиях динамика идеального газа описывается следующими формулами :
1) обобщенным уравнением Бернулли
-vdp=cdc+dlвнеш+ dlтр;
2) уравнением сохранения энергии
dqвнеш=срdT+cdc+dlвнеш;
3) уравнением неразрывности газового потока
которое после логарифмирования и последующего дифференцирования примет вид
4) уравнением состояния идеального газа Клапейрона pv=RT, которое после логарифмирования и последующего дифференцирования примет вид
Проведя совместное решение указанных четырех уравнений, получим соотношение:
В уравнении (1) левая часть содержит число Маха (М) потока и относительное изменение скорости газового потока. В правой же части представлены возможные влияния на поток, среди которых соответственно геометрическое, расходное, тепловое, механическое воздействия и влияние трения. Приведённое уравнение позволяет проанализировать влияние каждого из воздействий на характер изменения скорости дозвукового (при М<1) и сверхзвукового (при М>1) потоков. Рассмотрим особенности влияния каждого из воздействий. При этом условимся: рассматривая влияние одного из воздействий, остальные полагаем отсутствующими. При этих условиях общее уравнение (1) будет трансформироваться в частные уравнения применительно к каждому виду воздействия.
Влияние геометрии на газовый поток достигается путем изменения площади поперечного сечения канала вдоль проточной части.
Для описания данного воздействия применим уравнение (1). Здесь dF ≠ 0, а остальные воздействия считаются отсутствующими, т.е. dG=0; dqвнеш =0; dlвнеш dlтр=0. Следовательно, будем иметь
Полученное частное уравнение (2) выражает связь между скоростью движения газа и влиянием геометрии канала на поток.
Геометрическое воздействие на газовый поток широко используется в ГТД и других технических устройствах.
Расходное воздействие на поток осуществляется путем подвода к потоку извне или отвода от него вовне части газа.
Для описания данного воздействия применим уравнение (1). Здесь dG≠0, а остальные воздействия отсутствуют, т.е dF=0, dqвнеш=0; dlвнеш=0; dlтр=0. Следовательно, будем иметь
Уравнение (3), являясь частным, выражает связь между скоростью движения газа с расходным влиянием на газовый поток.
Поскольку по условию рассмотрения расходного воздействия геометрическое воздействие отсутствует, то, взяв интеграл от выражения dF=0, получим F= const, указывающее на то, что расходное сопло представляет собой канал с неизменными площадями поперечных сечений по его длине, в частности цилиндрический канал (рис. 1).
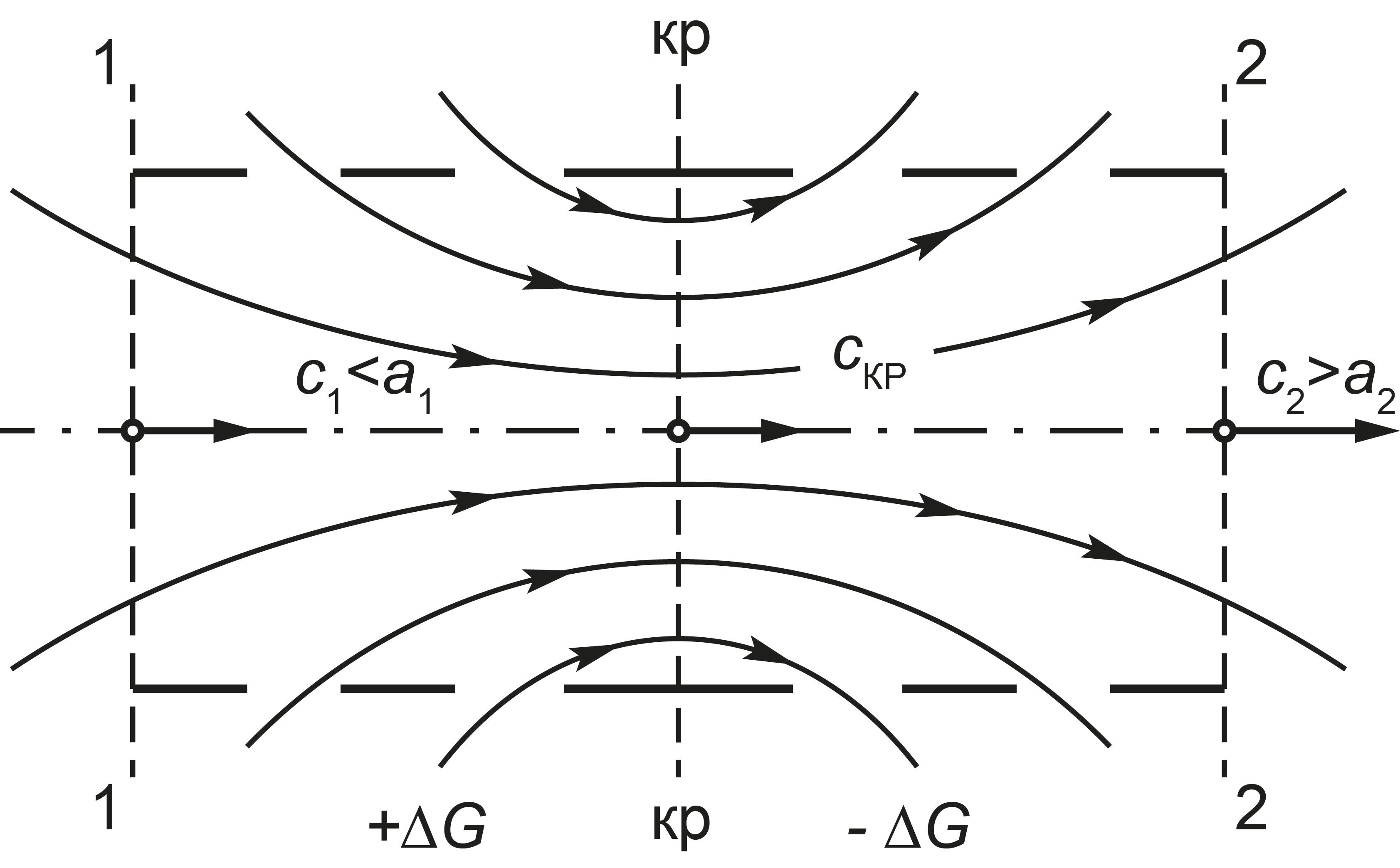
Рисунок 1 - Схема расходного сопла
Воспользуемся уравнением (3) для анализа течения газа в расходном сопле. В силу того что сопло предназначено для разгона газового потока, то для него всегда знак dc положителен (dc>0). Выясним, как нужно воздействовать на дозвуковой поток с тем, чтобы разогнать его в расходном сопле. Из уравнения следует, что при М<1 выражение в скобках будет отрицательным, т.е. (М2-1) < 0. Следовательно, общий знак левой части уравнения окажется отрицательным. Чтобы уравнение в целом выполнялось, должна быть отрицательной и его правая часть. Но последняя уже имеет знак минус, поэтому общий ее знак будет положительным, т.е. будем иметь dG>0. Отсюда следует вывод: для разгона дозвукового потока в расходном сопле к потоку извне нужно подводить газ.
Проведя аналогичные рассуждения применительно к сверхзвуковому потоку (М> 1), придем к выводу: для разгона сверхзвукового потока знак расходного воздействия на поток нужно изменить на обратный (dG<0), т.е. от потока нужно отводить часть газа вовне. В каком-то сечении расходного сопла будет иметь место соотношение с=а=скр=(М=Мкр), т.е. это сечение будет являться критическим.
Физически влияние эффекта расходного воздействия на поток, обеспечивающего его разгон, объясняется тем, что вначале подвод (вдув), а затем отвод (отсос) газа придают потоку профиль, эквивалентный соплу Лаваля. На практике расходное воздействие имеет место в ракетных двигателях твердого топлива (РДТТ)
. Но здесь реализуется только разгон дозвукового потока.Если обеспечить подачу газа со сверхзвуковой скоростью и отвод с дозвуковой, это может привести к замедлению потока.
Тепловое воздействие на газовый поток осуществляется путем подвода к потоку извне или отвода от него вовне теплоты. Для описания данного воздействия применим уравнение (1). Здесь dqвнеш ≠0, а остальные воздействия отсутствуют, т.е. dF=0; dG=0; dlвнеш =0; dlтр=0. Следовательно, будем иметь
Уравнение (4), будучи частным, выражает связь между скоростью течения газового потока с тепловым влиянием на поток. Так как в рассматриваемом случае геометрическое влияние отсутствует (dF=0), то тепловое сопло тоже представляет собой канал с постоянной площадью поперечного сечения (F=const), в частности цилиндрический канал (рис. 2).
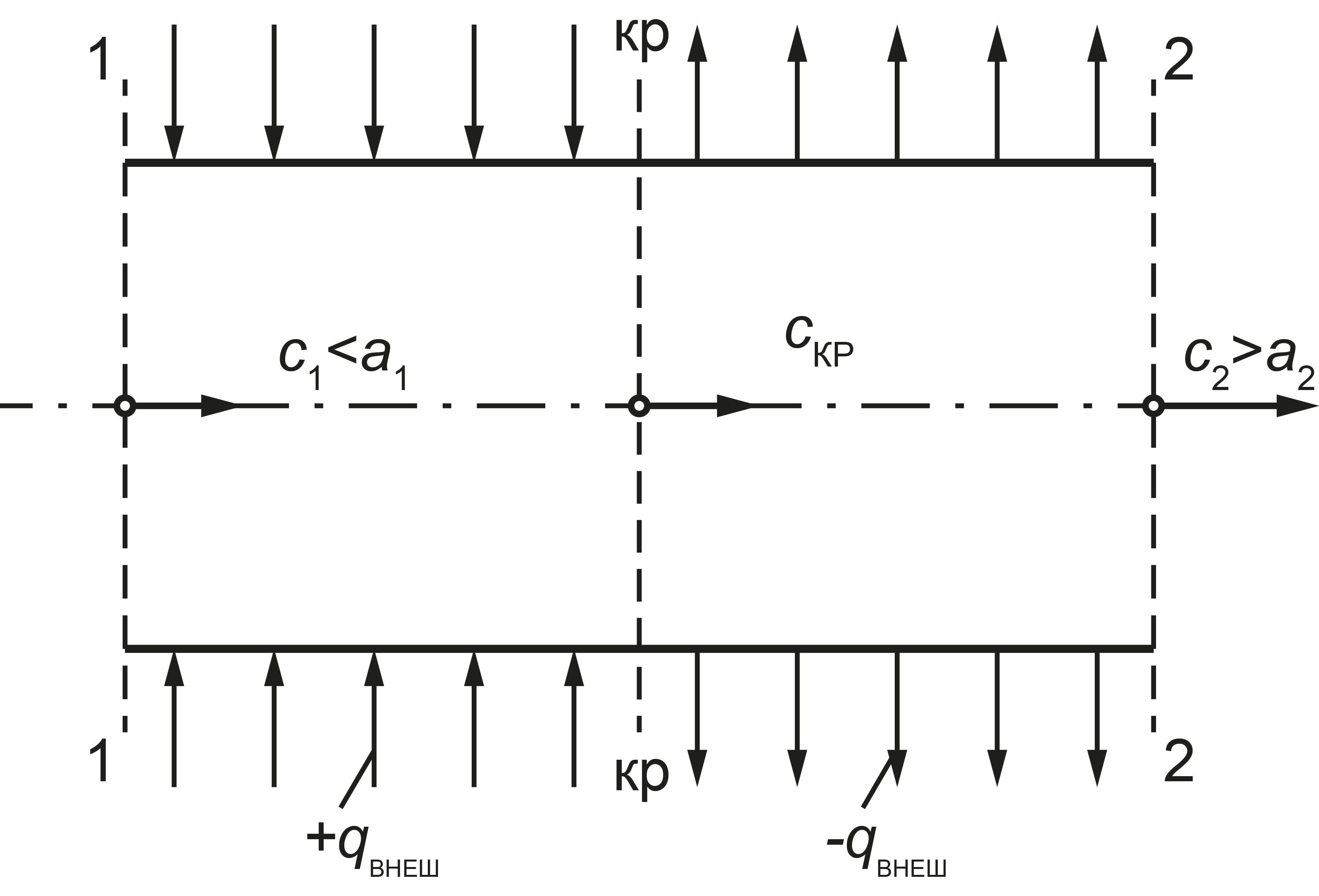
Рисунок 2 - Схема теплового сопла
Проведя аналогичные рассуждения применительно к сверхзвуковому потоку (М>1), можно установить, что для разгона сверхзвукового потока в тепловом сопле знак теплового воздействия на поток нужно изменить на обратный (dqвнеш < 0), т.е. от потока нужно отводить теплоту вовне. В каком-то сечении теплового сопла будет иметь место соотношение с=а=скр (М=Мкр=1). Это сечение будет являться критическим.
На практике тепловое воздействие на газовый поток имеет место, в первую очередь, в камерах сгорания ГТД (основных и форсажных), где осуществляется интенсивный подвод к газу (рабочему телу) располагаемой теплоты (q1) за счет сжигания топливовоздушной смеси
. В камерах сгорания поток дозвуковой, следовательно, при подводе теплоты он разгоняется.Имеет место на практике и отвод теплоты от потока. Это происходит, например, при охлаждении элементов конструкции ГТД и жидкостных ракетных двигателей (ЖРД)
. В первом случае в качестве охладителя используется воздух, забираемый в полете из окружающей среды, а во втором - один из компонентов топлива (горючее или окислитель). При охлаждении теплота передается от нагретого газового потока в стенку элемента конструкции, а от стенки к охладителю. Охлаждению подвергаются, естественно, элементы «горячей» части двигателей, например: газовая турбина, форсажная камера сгорания и реактивное сопло ТРДФ, ТРД, камера сгорания и реактивное сопло ЖРД и т.п. Характер влияния охлаждения элемента конструкции на течение газа в нем будет рассмотрен ниже на примере охлаждения стенок сопла Лаваля.Говоря о тепловом воздействии на поток, нужно отметить весьма важный момент, который может возникнуть при этом. Суть его в следующем. Когда теплота подается в дозвуковой поток внутри канала постоянного сечения, такого как цилиндрическая труба, поток ускоряется. Если число Маха потока достигает значения М=1, дальнейшее увеличение скорости больше не может быть вызвано добавлением теплоты (для этого необходимо было бы изменить направление воздействия, то есть отводить тепло, но в этом случае речь идет только об одном типе воздействия, положительном, то есть добавлении тепла). Возникает состояние, которое получило название тепловое запирание канала. В этом случае подвод теплоты после достижения потоком критической скорости приводит к уменьшению плотности газа (ρ) и так как скорость потока не изменяется (с=скр=акр=const), согласно уравнению неразрывности G=cρF=const секундный массовый расход газа через канал будет уменьшаться. Это явление называют тепловым кризисом. Данный кризис весьма нежелателен, потому что, например, в случае, когда поставлено условие сохранить расход газа, к потоку можно подвести лишь ограниченное количество теплоты.
Выше шла речь о разгоне потока путем теплового воздействия. Если подводится теплота при сверхзвуковой скорости потока и отводится его при дозвуковой скорости, то это приведет к замедлению потока.
Механическое воздействие на газовый поток осуществляется путем подвода к потоку извне или отвода от него вовне работы.
Для описания данного воздействия применим уравнение (1). Здесь dlвнеш ≠0, а dF=0; dG=0; dqвнеш =0; dlтр =0. Следовательно, будем иметь
Уравнение (5), являясь частным, выражает связь между скоростью движения газа с механическим влиянием на газовый поток. Прежде чем анализировать его, допустим, что работа считается положительной (dlвнеш>0), когда газ совершает работу (dυ >0), и отрицательной (dlвнеш<0), когда над газом совершается работа (dυ<0). Учтя это, из уравнения (5) следует, что если дозвуковой поток (М<1) совершает внешнюю работу (dlвнеш>0), то правая часть уравнения окажется отрицательной. Чтобы при этом уравнение выполнилось, должна быть отрицательной и левая часть уравнения. В левой части два сомножителя и чтобы она стала отрицательной, отрицательным должен быть один из них. Таким сомножителем является выражение в скобках [(М2-1)<0], так как по условию М<1. Следовательно, знак изменения скорости движения газового потока будет положительным (dc>0). Следовательно, если в дозвуковом потоке газ совершает работу, то поток при этом разгоняется. И, наоборот, при подводе внешней работы к дозвуковому потоку (dlвнеш<0) поток будет тормозиться (dc<0).
Если анализировать сверхзвуковой поток (М>1), то воздействие работы на поток будет обратным.
На практике газ совершает работу, например в турбинах ГТД, а подвод к газу работы осуществляется в компрессорах
.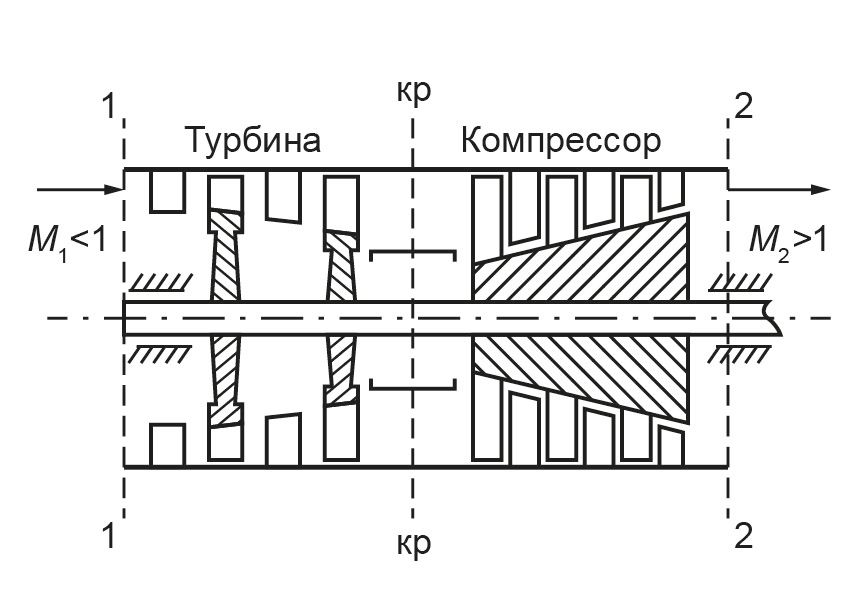
Рисунок 3 - Схема механического сопла
Для описания данного воздействия применим уравнение (1). Здесь dlтр≠0, а остальные воздействия отсутствуют, т.е. dF=0; dG=0; dqвнеш=0; dlвнеш=0. Следовательно, будем иметь
Уравнение (6), являясь частным, выражает связь между скоростью движения газа по каналу с влиянием трения на газовый поток. Проанализируем его. В приведённом уравнении работа, затрачиваемая на преодоление трения, имеет лишь один знак – она всегда положительна.(dlтр>0). Следовательно, правая часть уравнения всегда будет отрицательной. Чтобы уравнение выполнялось, должна быть отрицательной и левая часть, а это будет тогда, когда один из сомножителей, входящих в нее, будет отрицательным. Если рассматривать воздействие трения на дозвуковой поток (М<1), то отрицательным окажется выражение в скобках [(М2-1)<0]. Изменение же скорости будет положительным (dc>0). Последнее говорит о том, что под воздействием трения происходит разгон дозвукового потока.
Физическое воздействие трения на поток можно представить как тепловое воздействие. В соответствии с первым законом термодинамики, энергия, используемая для преодоления трения, полностью преобразуется в тепло (lтр =qтр), которое затем подводится к потоку. Как было установлено ранее, подвод тепла к дозвуковому потоку приводит к увеличению его скорости. Однако, необходимо учитывать, что увеличение скорости потока под действием трения (dc>0) приводит к уменьшению давления (dp<0).
Из уравнения (6) можно увидеть, что такое снижение будет более выраженным, чем при аналогичном увеличении скорости потока без трения за счет других влияний (таких как геометрическое), что объясняется рассеянием (диссипацией) энергии в движущемся потоке с трением и проявляется в снижении полного давления газа (p*) вдоль длины канала (что касается полной температуры T*, то она остается одинаковой, так как энергия, используемая для преодоления трения, преобразуется в тепло, которое затем подводится к газовому потоку).
Если рассматривать воздействие трения на сверхзвуковой поток (М>1), то в левой части уравнения (6) выражение, стоящее в скобках, окажется положительным [(М-1)>0] и чтобы левая часть уравнения стала отрицательной, должно быть отрицательным изменение скорости поиска (dc<0). Это означает, что под воздействием трения сверхзвуковой поток тормозится. Действительно, если к сверхзвуковому потоку подводить теплоту (в данном случае qтр), то, как это было установлено при рассмотрении теплового воздействия на поток, поток будет тормозиться.
В реальных условиях течения газа в элементах конструкции поток может подвергаться влиянию нескольких воздействий одновременно. При этом суммарный эффект воздействия будет зависеть от знака каждого воздействия.
3. Заключение
В заключение рассмотрения воздействий на газовый поток еще раз подчеркнем, что посредством внешних воздействий на поток его можно либо разогнать (dc>0), либо затормозить (dc<0). Однако при переходе через критическую скорость, соответствующую числу Маха М=1, знак любого из перечисленных воздействия нужно изменить на противоположный.
