МЕТОД РЕДУКЦИИ ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ СТАТИЧЕСКОГО СОСТОЯНИЯ КОНСТРУКЦИЙ С ГАЗОСТАТИЧЕСКИМИ ПОДШИПНИКАМИ
МЕТОД РЕДУКЦИИ ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ СТАТИЧЕСКОГО СОСТОЯНИЯ КОНСТРУКЦИЙ С ГАЗОСТАТИЧЕСКИМИ ПОДШИПНИКАМИ
Аннотация
Изложен метод упрощения процедуры решения систем нелинейных алгебраических и трансцендентных уравнений, описывающих нестационарное состояние газостатических подшипников. Проведён анализ общей модели статического состояний газостатических подшипников и приведён пример математической модели статического состояния осевого газостатического подшипника с двойным дросселированием газа в магистрали нагнетания газовой смазки. В результате проведенного анализа показано, что всегда существует возможность редукции исходной нелинейной системы к последовательности подзадач меньшей сложности. Предложенный подход позволяет уменьшить число уравнений, а в оптимальном случае преобразовать их в расчетные формулы. Рассмотрен пример системы, для которой найден идеальный способ ее решения посредством редукции уравнений к расчетным формулам.
1. Введение
В металлорежущих станках и контрольно-измерительных приборах находят применение конструкции газостатических подшипников скольжения
, , , , . Такие подшипники применяются в контрольно-измерительном оборудовании (координатно-измерительных машинах, кругломерах, высотомерах и т. п.), а также в качестве опорных элементов в шпиндельных узлах металлорежущих станков.Газостатические подшипники смазываются сжатым воздухом, поступающим от источника в проточный тракт, в котором могут использоваться, как пассивные, так и активные элементы ограничения потока газа в виде простых или кольцевых диафрагм, мембран, подвижных элементов иного вида для создания определенного давления, которое необходимо для поддерживания действующей нагрузки и контролируемого смещения подвижной части конструкции, обеспечивая тем самым ее низкую податливость несущего газового слоя, в том числе нулевую, а при необходимости в целях повышения точности металлообработки и отрицательную податливость
, .Одной из основных задач, которая ставится при исследовании подобных конструкций, является расчет их статических характеристик. Такие характеристики могут быть определены решением систем нелинейных алгебраических или трансцендентных уравнений, содержащих ряд факторов, к числу которых относятся давления в магистрали нагнетания на выходе ограничителей расхода, воздушные зазоры в несущем слое и регуляторах давления, перемещения подвижных элементов, несущая способность, расход смазки и др. Общее количество таких уравнений и факторов даже для самых простых конструкций составляет 2–4 нелинейных уравнения и 5–7 фактора, а для сложных конструкций шпиндельных узлов с подшипниками отрицательной податливости число таких уравнений может доходить до 8–10, а число факторов и того больше.
2. Методы и принципы исследования
Математическая модель статического состояния каждой конструкции газостатического подшипника представляет собой систему нелинейных уравнений, которую в общем случае можно записать в виде
где xj — факторы (статические характеристики), j = 1, 2, …, n–1, n; fi — функции, i = 1, 2, …, m–1, m.
Даже если бы такая система уравнений содержала всего лишь одно нелинейное уравнение, то решение такой задачи само по себе представляло бы определенную трудность, поскольку для этого необходимо было бы разработать и применить численный метод, например, метод Брента
, метод половинного деления или метод золотого сечения (если для решения используются методы оптимизации). Затем вычислив неизвестный фактор, на основании решения этого уравнения потребовалось бы найти остальные факторы при помощи расчетных формул.Когда система содержит два и более нелинейных уравнений расчет факторов превращается в достаточно сложную задачу вычислительной математики. В таких случаях выход зачастую пытаются найти применением общих численных методов решения нелинейных уравнений, к числу которых относятся методы итераций
, метод Зейделя , итерации Пикара , метод Ньютона , метод Ньютона-Рафсона , метод Бройдена и их модификации. Как показывает опыт, проблема состоит в том, что даже при удачном начальном значении вектора неизвестных критериев первых два метода сходятся слишком медленно либо расходятся. Методы ньютоновского типа могут также расходиться поскольку функции расхода через дроссели не являются гладкими, чем и объясняется расходимость данных методов.Вместе с тем, основываясь на опыте большого числа решенных для конструкций с газостатическими подшипниками задач специальными, учитывающими специфику систем уравнений методами, можно утверждать, что практически всегда существует возможность редукции общей системы нелинейных уравнений к системе с меньшим числом уравнений или даже сведения ее к последовательности формул для расчета неизвестных факторов, не обращаясь к общим методам решения систем нелинейных уравнений
, , , , , .Число n факторов в конструкциях газостатических подшипников всегда больше числа m уравнений, описывающих их статическое состояние (n > m), поэтому одну часть факторов задают, а другую часть рассчитывают посредством решения соответствующей системы нелинейных уравнений. Идею алгоритмической редукции такой системы, как методологического приёма преобразования упомянутой задачи к более простой и легче поддающейся решению форме, проиллюстрируем на примере расчета статических характеристик математической модели газостатического подшипника с одним дросселем в виде системы питающих кольцевых диафрагм .
На рисунке 1 представлена расчётная схема конструкция осевого газостатического подшипника.
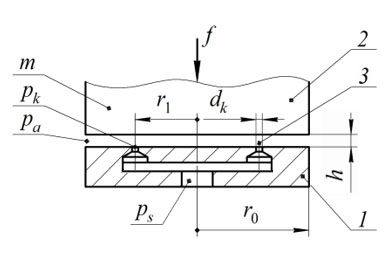
Рисунок 1 - Расчетная схема газостатического подшипника
Примечание: 1 – его корпус, 2 – подвижный элемент, 3 – дросселирующие отверстия диаметра dk
где функция истечения Прандтля
Формулы (2), (3) содержат связи расходов с давлениями Ps и Pd на входе и выходе диафрагм, радиусом R1 расположения питающих диафрагм, воздушным зазором H и критерием подобия диафрагм Ad. Интегральная формула (5) одновременно является уравнением связи несущей способности с давлением на выходе кольцевых диафрагм Pd и радиусом R1.
В результате несложных преобразований математической модели в ней осталось 2 нелинейных уравнения (4) и (5) и расчетные формулы (2) или (3) и (6), поскольку расходы Qh и Qh равны.
Факторами статического состояния подшипника являются n = 9 безразмерных переменных: зазор H, радиус R1, критерий Ad, давления Pd и Ps, силы W и F, расходы Qd и Qh. Сама модель статического состояния подшипника теперь является системой из двух нелинейных уравнений (4) и (5), в которых нужно так разделить 9 факторов на входные и выходные чтоб система была корректно решена посредством редукции её к двум расчетным формулам.
Идея алгоритмической редукции системы уравнений к более простому методу решения системы заключается в том, чтобы найти такой набор или конкурирующие наборы сочетания входных параметров, при котором систему из двух нелинейных уравнений можно было бы свести к минимальному числу уравнений. Важно, чтоб часть уравнений допускала бы их преобразование в формулы, при помощи которых можно было бы вычислить другие неизвестные факторы. Например, если бы в результате преобразований входными или вычисленными оказались такие факторы, как радиус R1 и давление и Pd, то из уравнения (5), которое превращается в формулу, можно было бы численным интегрированием вычислить несущую способность W, а через нее на основании (1) найти внешнюю силу F. Возможны и другие подобные варианты, указывающие на принципиальную возможность существования упрощающих решение задачи посредством упомянутой редукции.
3. Основные результаты
Чтобы система нелинейных уравнений была корректной число уравнений должно быть равно числу неизвестных. Поскольку в нашем случае уравнений два, то и неизвестных должно быть столько же. Таким образом, прежде чем приступить к решению системы уравнений (4) – (5) из 9 факторов следует выбрать только 2. Сделать это можно разными способами, их число, очевидно, равно вариантов сочетания входных и выходных факторов. Лучшие с точки зрения допустимой максимальной редукции варианты подлежат анализу с целью выбора одного или нескольких их них для последующей реализации вычислительного алгоритма решения системы (3) – (4) с наименьшими трудностями.
Критериями отбора являются сочетания, при которых таблица будет содержать наибольшее число строк, в которых все кроме одного факторы являются входными (1), а один (0) неизвестный является автономным и из такого уравнения можно с той или иной степенью сложности найти этот неизвестный фактор, не решая всю систему. Теперь такой фактор становится известным и, возможно, с учетом этого вновь открывшегося обстоятельства станет возможным решить новые автономные уравнения, что в свою очередь откроет новые возможности и так до тех пор, пока в идеальном случае не будет решена вся система нелинейных уравнений.
Нередко наперед известно какие факторы предпочтительно назначить входными. Например, для системы (4) – (5) это критерий Ad, радиус R1, давление наддува Ps. Впрочем, любой из них выбран в качестве рассчитываемого. В данном случае число факторов уменьшится и станет равным n = 3. Количество различных сочетаний варьируемых факторов H, Pd, W будет равно . Поскольку в системе (4) – (5) уравнений два, а неизвестных факторов три, то можно попеременно задавать значение только одного из них, пытаясь найти два других посредством редукции к системе уравнений меньшего порядка либо к вычислительным формулам с последующим расчетом по ним оставшихся неопределенных факторов.
4. Обсуждение
Можно выделить три основных способа упрощения процедуры решения системы нелинейных уравнений статического состояния исследуемого газостатического подшипника.
Способ 1. Зададим неопределенный фактор H, положив, например, H = 1. Этот фактор входит в только уравнение 4, в котором теперь остается лишь один неизвестный фактор давление Pd, который как видно, можно найти лишь решив нелинейное уравнение. К формуле в данном случае это уравнение не сводится. И хотя решить такое уравнение не представляет серьезной проблемы, данная процедура значительно сложнее процедуры вычисления по формуле. После определения давления Pd можно обратиться к уравнению (5) найти по формуле численным интегрирование несущую способность W, внешнюю силу F по формуле (6), расходы Qh и Qd по формулам (3), (1) и тем самым задача будет решена. Недостатком данного способа является потребность в решении одного нелинейного уравнения.
Способ 2. Результаты расчетов будем сводить в таблицу 1. Теперь зададим фактор Pd, положив, например, Pd = 0,7Ps (в таблице 1 это фактор второй очереди расчётов). Уравнение (4) теперь можно преобразовать в формулу и, используя её, затем вычислить зазор H (третья очередь определения фактора в таблице 1):
Фактор Pd входит в оба уравнения (4) – (5), поэтому в уравнении (5) теперь все факторы, входящие в интеграл, известны и интегрированием (5) можно определить несущую способность подшипника W (четвертая очередь определения фактора), затем на основании (6) внешнюю силу F (пятая очередь определения фактора). И, наконец, определим расходы газа Qd и Qh по формулам (2) и (3) (шестая и седьмая очереди).
Таблица 1 - Факторы математической модели подшипника
Факторы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
Ad | R1 | Ps | H | Pd | W | F | Qh | Qd | ||
Уравнения | 1 | 1 | 1 | 1 | 3 | 2 |
| 5 | 6 | 7 |
2 |
| 1 |
|
| 2 | 4 | ||||
Способ 2 не имеет недостатков, ибо позволяет идеально выполнить редукцию системы из двух нелинейных уравнений к двум расчетным формулам.
Способ 3. Наконец, зададим неопределенный фактор W. Данная попытка самая неудачная, потому что, во-первых, задать реальное числовое значение несущей способности достаточно затруднительно исходя из технических соображений и, во-вторых, при этом пришлось бы решать нелинейное интегральное уравнение, которое даже сложнее того уравнения, которое пришлось бы решать первым способом. Отметим, что попутно пришлось бы решать и уравнение (4), поскольку ни давление Pd ни зазор H не определены. По сути, способ приводит нас к задаче для нелинейной системы с двумя неизвестными, то есть самой сложной задаче из числа возможных.
Таким образом, наилучшим методом решения системы нелинейных уравнений, который позволил решить ее в идеальном виде, является способ 2, при помощи которого удалось решить систему нелинейных уравнений посредством редукции ее к последовательности расчетных формул.
5. Заключение
В статье изложена идея упрощения процедуры решения систем нелинейных алгебраических и трансцендентных уравнений, описывающих нестационарное состояние газостатических подшипников. Её суть состоит в возможности редукции исходной нелинейной системы к последовательности подзадач меньшей сложности. Предложенный подход позволяет уменьшить число уравнений, а в идеальном случае преобразовать их в расчетные формулы. Рассмотрен пример системы, при решении которой найден наилучший способ ее решения посредством редукции уравнений к расчетным формулам. Описана общая методика редукции нелинейных систем к более простым подзадачам и метод их решения.
В результате анализа предложенного подхода установлено, что в общем случае идея редукции нелинейных систем, для которых число факторов всегда превышает число уравнений, может быть осложнена рядом специфических особенностей, затрудняющих нахождение наилучшего сочетания входных и выходных факторов, при которых система может быть решена с наименьшими трудностями. В частности, не всякий набор входных факторов является допустимым, что выявляется непосредственно либо в результате последовательного анализа состояния каждого уравнения системы. На наш взгляд, основной проблемой является разработка многокритериальной оценки оптимального набора входных факторов, при котором обеспечивается быстрое решение системы с минимальными затруднениями. Данной актуальной проблеме предполагается посвятить отдельную статью.
